Předpověď vzniku události

Prahem rozumíme dosažení a překročení kritické hodnoty nějakého měřitelného prvku (například srážkového úhrnu), kdy lze očekávat vznik nepříznivé události. Obvykle je ale takových prvků více. Musíme tedy sledovat i jejich kombinace, resp. kombinace jejich kritických hodnot.

Příkladem může být předpověď povodně při dosažení limitu srážkových úhrnů pro kritickou úroveň nasycení půdy v krajině. Totéž platí pro tzv. mělké sesuvy, které reagují na bezprostřední srážky, ale mohou se vyskytnout pouze na svazích a na k sesouvání náchylném podloží.

Předpověď intenzity a rozsahu událostí na základě známých dat s sebou nese jeden filozofický problém. Nevíme totiž, zda dostupná data popisují celý možný rozsah událostí, které se reálně mohou vyskytnout. I když máme představu o druhu nebezpečí, nelze již s jistotou předpovědět maximální intenzitu. Velmi názorný příklad vlivu neznámých faktorů představil N. Taleb ve své známé publikaci Černá labuť. Přestože se práce věnuje převážně finančnímu světu, spadají sem i neočekávané dopady mimořádně intenzivních přírodních pohrom, viz Fukušima.

Metody určení prahových hodnot

Přírodní procesy se sledují dlouhou dobu. U mnoha z nich proto existují rozsáhlé databáze a dlouhé časové řady. Příkladem mohou být časové řady teplot vzduchu (např. Praha Klementinum od 1775), průtoků a vodních stavů nebo obecně počasí. Analýzou výskytu přírodních pohrom v takových řadách jsme schopni odhadnout prahové hodnoty měřitelných prvků.

Regrese

Nejjednodušším způsobem je v takových případech využití regrese. Vysvětlovanou proměnnou (např. spadl/nespadl sesuv, x-letost povodně) se snažíme vyjádřit pomocí vysvětlujících proměnných, které lze snadno změřit nebo jsou známy z databáze (např. množství srážek, sklon svahu). Často používanou je lineární regrese (pro spojitou vysvětlovanou proměnnou) a logistická regrese (pro binární vysvětlovanou proměnnou). Více informací o regresi lze nalézt např. v Anděl (1985).

Vycházíme z dostatečného množství dat (to je základní podmínka), přičemž umíme odhadnout práh vysvětlované proměnné. Prahy mohou být v principu dva, a to spodní (lower boundary), pod kterým se daný negativní jev nikdy nevyskytl a horní (upper boundary), nad nímž se daný jev vyskytl vždy. Mezi těmito prahy se nachází interval, ve kterém se zvyšuje pravděpodobnost, že při dosažení dané hodnoty měřeného prvku vznikne přírodní pohroma.

Využití regrese se hodí tehdy, když nemáme jasnou představu o všech faktorech, které se mohou na vzniku jevu podílet. Nemůžeme tedy sestavit procesní model. Víme však, že jev vzniká při dosažení kritické hodnoty jednoho nebo několika prvků. Jestliže máme dostatek dat z minulých událostí, potom se můžeme pokusit odhadnout závislost jevu na těchto vstupních datech.

Výsledkem je regresní funkce. Jedná se o běžný postup v přírodních vědách. Jenom pro sesuvy bylo podobných schémat uděláno několik (například Guzzetti et al., 2007). Obvykle platí známý vztah pro lineární regresi, např.:

y = ax + b

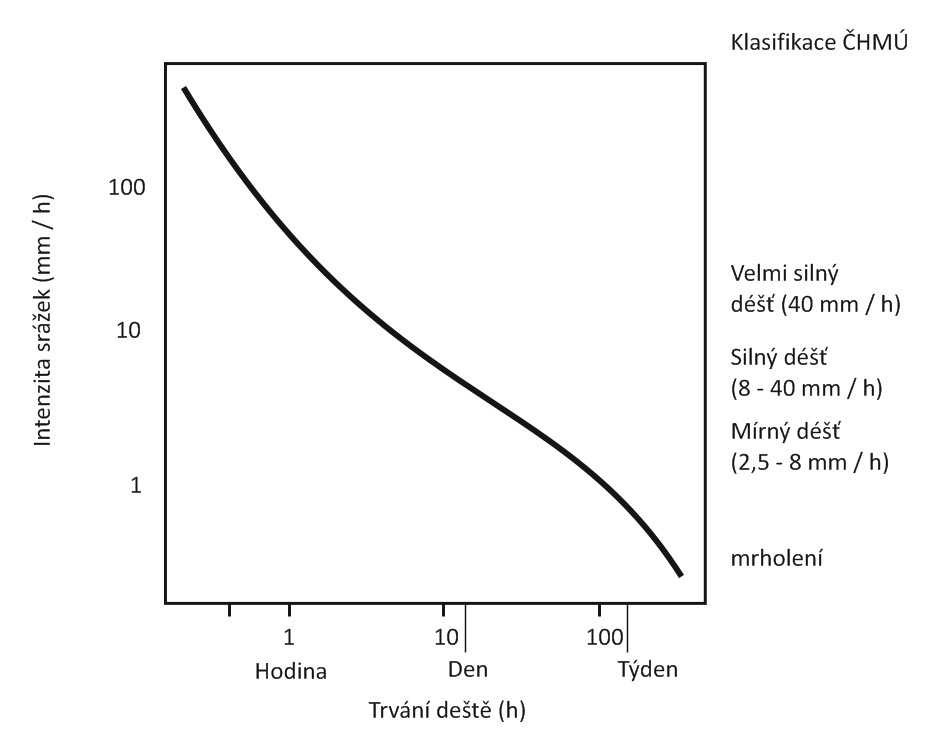
Vztah mezi intenzitou a trváním deště. Prostor vymezený oběma osami není v realitě rovnoměrně zastoupen, co se týká četnosti výskytů srážkových událostí. Velmi intenzívní a dlouho trvající deště se ve skutečnosti nevyskytují. Obecně platí, že srážky s vysokou intenzitou mají krátké trvání a naopak srážky málo intenzívní mohou trvat delší dobu. Uvedená linie může představovat práh, nad nímž může docházet ke vzniku přívalových povodní, sesuvů apod.

V případě, že známe dobře mechanismus vzniku jevu, můžeme použít procesní modelování.

Procesní modelování

Procesí modely vyžadují přesné vstupy. Obvykle se jedná o modely deterministické, některé z nich však mohou pracovat též se stochastickými daty. To znamená, že některá ze vstupních hodnot není známa a musí být nahrazena například intervalem hodnot s určitým rozdělením pravděpodobnosti, ze kterého se konečná hodnota pro model vybere. Výběr lze provádět pomocí dalších náhodných metod, kdy se respektuje předem dané rozdělení hustot pravděpodobností.

Od regresních modelů se modely procesní zásadně liší tím, že simulují fyzikální procesy. U regrese nás zajímá pouze vztah mezi vstupy (změřené hodnoty) a objevením se jevu (např. vznik sesuvu). Aby byl procesní model užitečný a pomohl v předpovědi, musí pro něj platit následující: zahrnuje všechny podstatné vstupy, u všech jsme schopni změřit nebo jinak určit jejich hodnoty. Stále však budeme vystaveni nebezpečí, že námi dosud zaznamenaná časová řada nebude obsahovat všechny fyzikálně přípustné stavy daného procesu. To znamená, že nebudeme brát do úvahy extrémy, jelikož se dosud v našich datech nevyskytly.

Tento druh modelů je velmi závislý na vstupních datech. Ta obvykle nejsou dostupná mimo pozorované území a modely tak mohou být nepřenositelné. Detailní poznání všech faktorů v novém prostředí (např. geologická stavba, mocnost a vlastnosti zvětralin, koeficienty infiltrace, úhly vnitřního tření zemin apod.) je obvykle nemožné a vždy finančně velmi nákladné. Z tohoto důvodu jsou aplikace zejména komplexních modelů velmi nedůvěryhodné.

Studium historických pramenů a denního tisku

V některých případech nemáme k dispozici řady instrumentálních dat a musíme si vystačit s kusými informacemi v podobě zápisů z kronik, novin nebo neperiodických zpráv. Můžeme použít analogie s jiným územím, jestliže mají obě nějaké společné znaky.

Tato práce je časově dosti náročná a závislá na stupni zachování těchto zdrojů. Velmi se liší místo od místa, a to i v rámci jednoho území nebo státu. Kronikáři zapisovali obvykle události, které byly něčím mimořádné nebo postihly osoby a majetky. Vzhledem k tomu, že například v Karpatech je sesouvání poměrně běžnou záležitostí, nemusela být těmto jevům, pokud se neprojevovaly zvláště ničivě, věnována taková pozornost, jako v jiných částech země.

Kdy lze nebezpečí očekávat?

Některé jevy mají pravidelný chod, protože jsou závislé na oběhu Země kolem Slunce, nebo na střídání dne a noci. Více méně pravidelně se proto vyskytují mrazy, letní požáry, jarní tání a s ním spojené povodně a sesuvy, letní povodně z bouřek apod. Taková cykličnost je srozumitelná a lidé se na ni jsou schopni připravit. Mnohá lidová rčení takové cykly obsahují, resp. si všímají prekurzorů slabých nebo silných událostí. Velmi poučnou práci na téma meteorologických pranostik zpracoval Munzar (1986).

Jiné pohromy jsou z pohledu výskytu v čase nepravidelné až náhodné, což je například zemětřesení nebo vulkanismus. Procesy, které je spouštějí, mají vlastní dynamiku a není snadné je monitorovat a modelovat, a proto se nám mohou zdát jako náhodné. Je však zřejmé, že zemětřesení mají přímý vztah k procesům deskové tektoniky, stejně jako vulkanismus.

Z uvedeného výčtu je zřejmé, že do první skupiny jevů patří ty jevy, jejichž počátek je zakotven v chodu počasí a místním klimatu – jsou do jisté míry predikovatelné. Jestliže nebudou v létě měsíc žádné srážky, potom lze očekávat požáry. Tím ničivější a závažnější, pokud se nejedná o území, kde jsou požáry pravidelné a neprojevují se ničivě.

Rovněž jarní tání sněhu můžeme považovat za pravidelný jev, který nemusí způsobit povodně a případně sesuvy půdy. Již dopředu lze odhadnout vodní obsah sněhu a porovnat aktuální zásobu s hodnotami z minulosti, pokud taková data jsou k dispozici.

Prahové stavy a fázové přechody

Mnoho přírodních procesů mění svoji podobu nikoliv plynule, ale skokem. V laboratořích byla modelována skoková změna říčního vzoru z meandrujícího na divočící (braided) v důsledku nepatrné změny sklonu údolního dna.

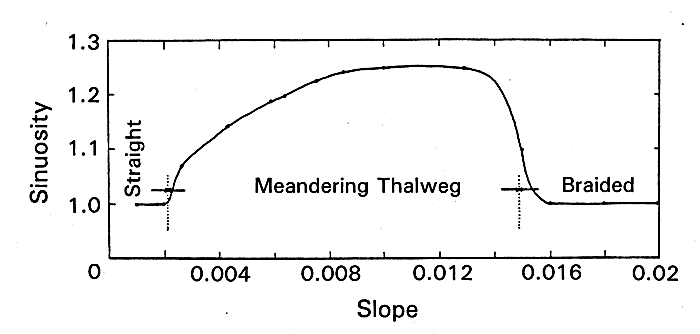
Změna říčního vzoru (Knighton, 1984)

Podobné fázové změny lze pozorovat v charakteru proudění v porézním prostředí. Dochází ke změně z plynulé difuzní infiltrace vody do půdy, případně jiného prostředí, na náhlý „puls“, kdy se relativně značný objem vázané vody v půdě vlivem gravitace uvolní a vyteče z půdního profilu (Fürst at al., 2009).

Je třeba si také uvědomit, že stávající modely jsou omezeny rozsahem vstupních hodnot a nelze pouze extrapolovat výsledky pozorování, ale v krajních případech je nutné počítat s fundamentální změnou chování systému (viz obr. Meandering).

Měřítko nebezpečí

Zatímco povodeň je vděčným předmětem zpravodajství, sucha nejsou tak atraktivní. Jsou to ale právě sucha, která do budoucna představují závažný problém. Žádná povodeň, ani ta nejextrémnější, nemá schopnost zničit a rozvrátit společnost. To však neplatí o suchu. Před povodní je možné v případě nouze utéci na nejbližší vrch. U rozlivů velkých řek lze alespoň v předstihu zmapovat jejich maximální rozsah a předem se připravit vhodnými opatřeními nebo ústupem do nezáplavových oblastí. Sucho nastává pozvolna. Pouze zemědělci, kterých je však v moderní společnosti velmi málo, si všímají, jak se postupně snižují zásoby podzemní vody.

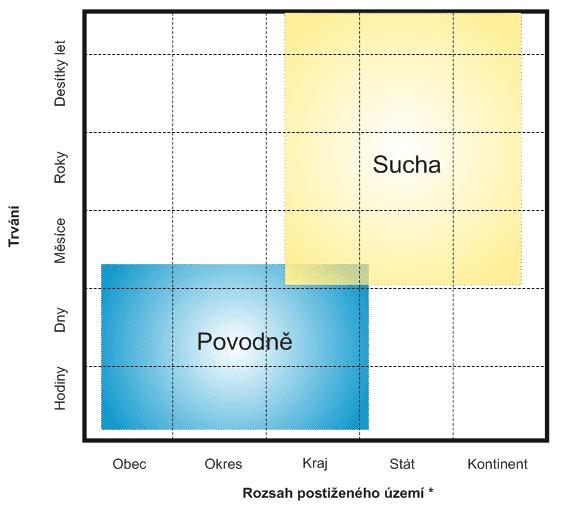
Příklad rozdílného trvání a rozsahu zasaženého území pro přírodní pohromy povodně a sucha. U povodní je třeba si uvědomit, že postihují území výhradně v okolí vodních toků, takže rozsah kraje znamená v podmínkách ČR v podstatě velmi malou plochu. Naopak povodně v deltách velkých řek mohou skutečně zasáhnout značná území.

Do budoucna lze předpokládat, že lidstvo bude muset zaměřit svou energii na efektivní hospodaření s vodou a případně na transport vody na velkou vzdálenost. Získávání pitné vody odsolováním, v přímořských oblastech s nadbytkem slunečního svitu, je výzvou v nejbližší budoucnosti.  

Intenzita nebezpečí

Intenzita přírodního procesu je obvykle závislá na dostupné energii, která se může uvolnit. V krajině se jedná zejména o energii potenciální, která se může přeměnit na kinetickou. Odhad potenciální energie a tedy i potenciální intenzity jevu můžeme jednoduše získat tak, že se podíváme, jaké je v krajině převýšení (energie reliéfu). Neplatí to vždy, ale v naprosté většině případů jsou bahnotoky a sesuvy větší a ničivější v Alpách než v Karpatech.

Výjimku tvoří například přítomnost ke ztekucení náchylných zemin, které se mohou vyskytovat v poměrně mírném až plochém terénu. Ke ztekucení těchto zemin dochází okamžitě, což je velmi nebezpečné. Příčinou mohou být otřesy, které vypudí z minerálních mřížek jílů slabě vázanou vodu, což způsobí skokové snížení vnitřního tření. Následkem je ztráta únosnosti takových zemin a kolaps staveb.

Intenzita procesu

Některé jevy jsou z podstaty binárního charakteru. Buď nastanou, anebo nikoliv. U jiných se plynule mění jejich intenzita a problémy nastávají až při překročení kritické úrovně.

Po zprávě o povodni obvykle následuje její rozsah. Když voda vystoupí z břehů, můžeme již začít hovořit o povodni. Kritickou úrovní je v tomto případě průtok vodního toku (m³/s), nebo snadněji měřitelný vodní stav (m). Až do stavu naplnění koryta se však nemusíme zneklidňovat, protože voda bude pořád odtékat v mezích agradačních povodňových valů. Problémy mohou nastat, pokud jsou takové valy nestabilní, poničené a nemohou poskytnout ochranu. Může dojít k jejich náhlému protržení, kdy se voda překotně rozlévá do nivy. Následky jsou potom katastrofální, pokud se tak stane v zastavěném území (viz případ New Orleans z toku 2005). V případě pochybností o možnosti naplnění takového scénáře je lepší přistoupit ke kontrolovanému zatopení území. Jakmile se vylije voda z břehů, sníží se celková rychlost jejího pohybu, protože v místech mimo vlastní koryto je mnohem větší odpor vůči proudění vody. Z toho důvodu je snaha stavět v obydlených a cenných oblastech vysoké protipovodňové valy, ale v místech polí, luk apod. co nejnižší. Vylití vody v takovém prostředí oddálí nástup a výšku kulminace povodně dále po toku.

Zatímco intenzita zemětřesení se vyjadřuje Magnitudem, v případě povodní se udává očekávaná výška vody v toku. Pro sníh můžeme použít očekávanou výšku nového sněhu, stejně jako mocnost pokrývky vulkanického materiálu v určité vzdálenosti od sopky. Svahové procesy mají různou intenzitu v závislosti na geologickém podloží, aktuálních srážkách, ale také na případné intenzitě umělého porušení svahu.

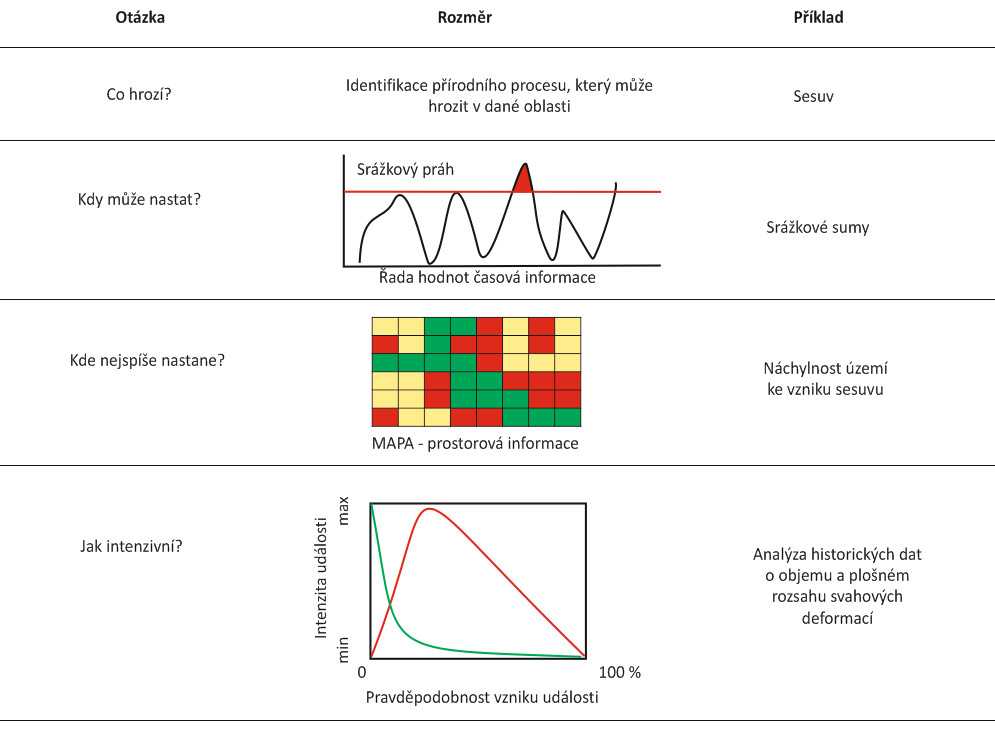
Komplexní hodnocení ohrožení přírodní pohromou musí zahrnovat všechny uvedené fáze. Zásadní je identifikace druhu nebezpečí, určení prahů, potenciálně zasažené lokality a intenzit procesů by mělo následovat.

Kombinované nebezpečí (multihazard)

Tímto pojmem označujeme výslednou hodnotu nebezpečí, která vznikne sloučením všech v území identifikovaných dílčích nebezpečí. Je totiž běžné, že se areály přírodních nebezpečí překrývají a je tudíž nutné vyjádřit celkovou pravděpodobnost, že se nějaké (aspoň jedno) z nich může objevit. Nejvíce ohrožená území jsou nejen pobřežní a horské oblasti, ale i území v okolí vulkánů.

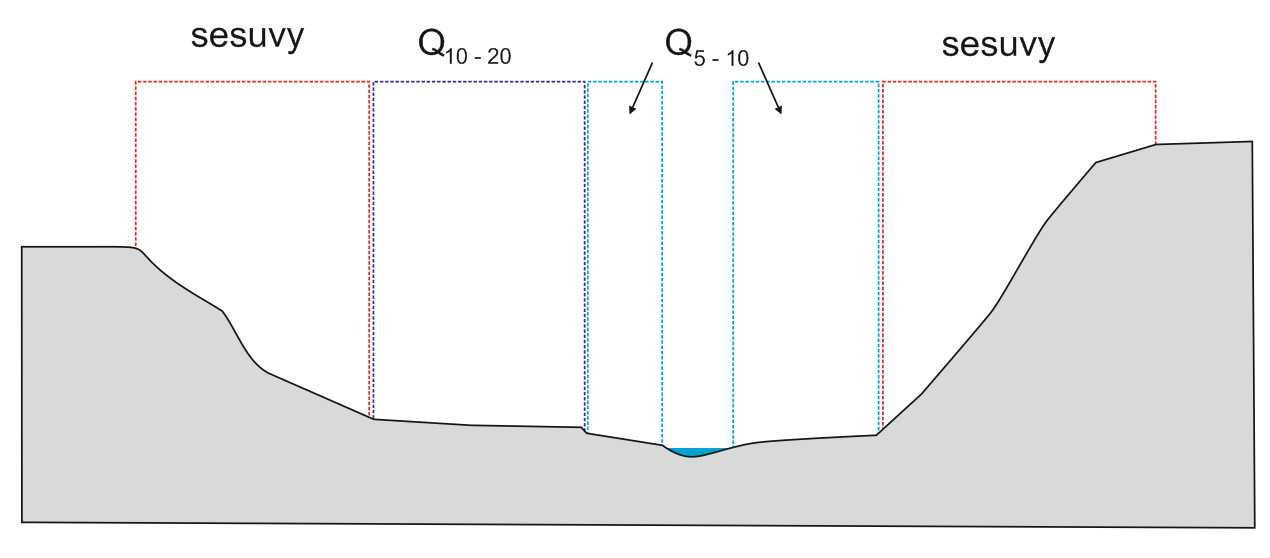
Na příkladu údolí, ve kterém je třeba počítat buď s povodní, nebo se sesuvem, lze demonstrovat, že někdy se nebezpečí nelze vyhnout. V takových případech se musíme věnovat metodám snižování nebezpečí. V praxi se pásy s výskytem sesuvů a povodní mohou překrývat

Smysl hodnocení a modelování přírodních procesů v jednom komplexním přístupu vyvstane tehdy, když si uvědomíme, že například sesuvy mají schopnost ovlivnit vodní tok. V extrémním případě mohou zahradit nejenom koryto toku, ale též celé údolí. Dopady takové událostí se potom přenášejí do oblastí proti toku řeky, protože vzniká zátopa v důsledku vzniku hráze z materiálu sesuvu. Případné protržení takové hráze zase může znamenat katastrofu na místech dále po toku.